[통계학] 이산확률분포 이해하기(베르누이, 이항, 기하, 음이항, 초기하, 포아송 with R)

이산확률분포와 연속확률분포의 차이는 뭘까?

확률분포

이산확률분포: 확률변수가 취하는 값들의 집합이 자연수의 부분 집합과 일대일 대응 됨

연속확률분포: 확률변수가 취하는 값들의 집합이 실수의 구간을 이룸

https://www.g2.com/articles/discrete-vs-continuous-data

위 나무위키의 설명은 직관적으로 이해하기 어려워서 예시를 들어 설명해보겠다!

대한민국 대학생의 몸무게를 확률변수 X라고 가정해보자.

여기서 확률변수 X는  60.5kg, 60.55kg, 60.555kg, 60.55555555 등 무수히 많은 몸무게를 가질 수 있다.

↑ 이렇게 연속적으로 확률변수를 많이 가진 확률의 분포를 연속확률분포라고 한다. (키, 발사이즈 등도 마찬가지)

 

반대로 동전던지기, 주사위 던지기처럼 확률변수가 가질 수 있는 값이 명확하고 셀 수 있는 경우의 분포를 이산확률분포라고 한다. (COUNT 개념이라면 보통 이산확률분포라고 보면 된다.)  지금은 이산확률분포에 대해 알아보자 !

 

이산확률분포

1. 베르누이 분포( Bernoulli distribution )

https://www.cuemath.com/data/bernoulli-distribution/

시행 횟수가 1회, 시행의 결과가 오직 두가지인 경우인 분포다.

p확률로 1(성공), 1-p의 확률로 0(실패)의 확률변수를 가지고 있다.

동전던지기의 앞면 성공, 복권 당첨, 시험 합격/불합격 등이  예시다.

베르누이 분포의 확률질량함수식

 

EX) 10개의 티켓 중 2개는 제주도행 당첨 티켓, 8개는 꽝이이다.

당첨 확률 p(1)는 (0.2)^(1) × (0.8)^(1-1) = 0.2 × 1 = 0.2

비당첨 확률 p(0)는 (0.2)^(0) × (0.8)^(1-0) = 1 × 0.8 = 0.8

2. 이항분포( Binomial distribution )

https://www.statsref.com/HTML/binomial.html

베르누이 분포가 1회 시행했다면, 이항분포는 성공확률이 p인 베르누이 시행을 n번, 독립시행한 분포다.

(※ 독립시행: 매번 같은 조건에서 시행을 반복하는 것, 예를 들어 주사위를 다음에 던질 때 똑같이 1/6 확률을 가짐)

p(성공확률)이 낮다면 위 그림(p=0.1)처럼 왼쪽, p(성공확률)이 높다면 그림(p=0.75)처럼 오른쪽으로 몰릴 것이다.

이항분포의 확률질량함수식

베르누이 분포와 이항 분포의 차이 한눈에 보기
베르누이 분포	이항 분포
베르누이 분포는 사건의 단일 시행 결과를 모델링할 때 사용	어떤 사건에 대한 여러 번의 독립시행 결과를 모델링할 때 사용
x~베르누이(p), p는 성공확률	x~이항식(n,p), n은 시행 횟수
EX) 시험 합격확률 80%, 불합격 확률 20%일 때, 베르누이 분포 사용	EX) 시험 합격확률 80%, 불합격 확률 20%일 때, 학생이 5번의 시험 중 4번 합격할 확률 구할 때 이항 분포 사용

 

3. 기하분포 ( Geometric distribution )

https://live.boost.org/doc/libs/1_48_0/libs/math/doc/sf_and_dist/html/math_toolkit/dist/dist_ref/dists/geometric_dist.html

기하분포는 성공확률 p인 베르누이 시행에서 처음 성공할 때까지의 시행횟수를 나타내는 분포다. 

기하분포의 확률질량함수식

p: 성공확률, x: 시행 횟수를 의미한다.

 

EX)

1. 빨간공을 뽑아야 당첨되는 이벤트에는 파란공이 9개, 빨간공이 1개가 있다. 복원추출하여  2번 째에 빨간공을 뽑을 확률을 R로 구해보자. <빨간공을 뽑을 확률: 0.1> (dgeom 함수 이용)

약 8.1%

2. 빨간공을 뽑아야 당첨되는 이벤트에는 파란공이 9개, 빨간공이 1개가 있다. 복원추출하여 3번째 안으로 빨간공을 뽑을누적확률을 R로 구해보자. <빨간공을 뽑을 확률: 0.1> (pgeom 함수 이용)

약 34.39%

위 확률은 다음 확률과도 같다.

4. 음이항분포( Negative binomial distribution )

https://www.statisticshowto.com/negative-binomial-experiment/

음이항 분포는 성공확률 p인 베르누이 시행에서 r번 성공할 때까지의 시행횟수를 나타내는 분포다.

음이항 분포의 확률질량함수식

EX)

1. 성공확률이 0.1인 제비뽑기에서 100번 실패하고 10번 성공할 확률을 R로 구해보자. (dnbinom 함수 이용)

약 1.13%

2. 성공확률이 0.1인 제비뽑기에서 100번의 실패를 허용하고 10번 성공할 확률을 구해보자. (pnbinom 함수 이용)

약 67.1%

음이항 분포와 기하 분포의 차이 한눈에 보기
기하 분포	음이항 분포
베르누이 시행에서 성공이 1번(처음)나올 때까지의 시행 횟수	베르누이 시행에서 성공이 r번 나올때까지의 시행 횟수
Geo(p) p는 성공확률	NB(r, p) r은 성공 횟수, p는 성공확률
성공이 아닌 실행횟수가 중요하고 첫 번째 성공이 중요할 때 사용한다.  EX)  x번째 시도(실행횟수) 중 n번째 안에 성공할 확률은?	실행횟수보다 성공횟수가 중요할 때 사용한다. EX) x번째 시도 중 n번 성공(성공횟수)할 확률은?

5. 초기하 분포 ( Hypergeometric distribution )

https://blogs.sas.com/content/iml/2020/04/06/geometric-distribution-sas.html

크기가 N인 모집단에서 비복원추출로 n개를 추출할 때, k번 성공할 확률에 대한 분포다.

초기하분포의 확률질량함수는 X ~ hypergeo(N, K, n)을 따르는데, 
N: 모집단 크기, K: 모집단에서 성공 원소의 개수 (N-K= 실패 개수), n: 비복원 추출되는 항목 개수(표본크기)를 의미한다.

초기하분포 확률질량함수식

EX)

1. 빨간공 5개, 파란공이 15개일 때, 3개를 비복원 추출해서 1개가 빨간공일 경우를 R로 구해보자. (dhyper 함수 이용)

약 46%

2.  빨간공 5개, 파란공이 15개일 때, 3개를 비복원 추출해서 1개가 빨간공일 경우를 R로 구해보자. (phyper 함수 이용)

약 86%

이 확률은 3개가 빨간공, 17개가 파란공, 3개를 비복원추출했을 때, 빨간공이 0개일 확률과 1개일 확률을 더한 값과 같다. 

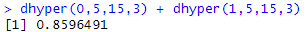
6. 포아송 분포( Poisson distribution )

https://www.scribbr.com/statistics/poisson-distribution/

포아송 분포는 주어진 기간 또는 공간 내에서 어떤 사건이 몇 번 발생할지를 표현한 이산확률분포다.

 

포아송 분포를 사용할 수 있는 조건은 다음과 같다.

1. 사건은 무작위, 독립적으로 발생한다. (즉, 한 사건의 확률은 다른 사건의 확률에 영향을 끼치지 않는다.)

2. 주어진 시간 또는 공간 내에서 발생한 사건의 평균 수를 알고 있어야 한다. 이는 곧 λ(람다)라고 하며 상수로 가정된다.

포아송분포 확률질량함수식

EX) 한 고객 센터에서 시간당 96건의 전화를 받는다고 가정하자.

이 정보를 가지고 5분 동안 전화가 0번 ~ 10번까지 걸려올 확률 포아송 분포 공식에 대입해 각각 구해보자. 

 

5분 동안의 전화 평균은 96 / 12(= 60/5) = 8이 된다!  이 8은 곧 λ(람다)가 된다.

이 λ(람다)를 이용해 R로 0번 ~ 10번까지 공식을 대입해보았다.

 

5분 동안 전화가 0번 걸려올 확률은 약 0.03%

5분 동안 전화가 1번 걸려올 확률은 약 0.2%

5분 동안 전화가 2번 걸려올 확률은 약 1%

5분 동안 전화가 3번 걸려올 확률은 약 2.8%

5분 동안 전화가 4번 걸려올 확률은 약 5.7%

5분 동안 전화가 5번 걸려올 확률은 약 9.1%

5분 동안 전화가 6번 걸려올 확률은 약 12.2%

5분 동안 전화가 7번 걸려올 확률은 약 13.9%

5분 동안 전화가 8번 걸려올 확률은 약 13.9%

5분 동안 전화가 9번 걸려올 확률은 약 12.4%

5분 동안 전화가 10번 걸려올 확률은 약 9.9%

 

Question) 그리고 여기서 만약에 전화가 2번 이상 걸려올 확률을 구하라고 한다면? 

5분 동안 걸려올 전화의 전체 확률 중 0번~1번 걸려올 확률을 빼주면 된다.

1 - ( 5분 동안 전화 0번 확률 + 5분 동안 전화 1번 확률) = 5분 동안 전화가 2번 이상 걸려올 확률(99.6%)

 

R 확률 분포 관련 함수 코드

확률분포	확률밀도 함수	확률누적 함수	분위수 함수
이항분포	dbinom	pbinom	qbinom
기하분포	dgeom	pgeom	qgeom
음이항분포	dnbinom	pnbinom	qnbinom
초기하분포	dhyper	phyper	qhyper
포아송분포	dpois	ppois	qpois

 

 

 

 

 

 

 

<참조자료>

http://infoso.kr/?p=3571

https://wikidocs.net/198756

https://thebook.io/006723/0239/